In this post I show you how to simulate an OOMMF hysteresis loop. You can follow this tutorial with more or less any OOMMF oxsi mif file, but I will be using a version of the oxsi exchspring.mif example file that comes with OOMMF, modified to automatically display some outputs.
Read more about OOMMF example files.
OOMMF Hysteresis Loops – The Zeeman Energy Term
In a physical, real-world experiment, a hysteresis loop would be made by ramping up and down a magnetic field. An OOMMF hysteresis loop is achieved in a similar way, by ramping up and down a Zeeman energy term.
The simplest way to include a Zeeman energy term in an OOMMF mif file is with an Oxs_UZeeman term which includes a uniform, homogeneous magnetic field to the simulation.
Read the official documentation about Zeeman terms in OOMMF.
In the exchspring.mif example, the Zeeman term is:
Specify Oxs_UZeeman [subst {
multiplier [expr {0.001/$mu0}]
Hrange {
{ 0 0 0 500 50 0 10 }
{ 500 50 0 -500 -50 0 20 }
{ -500 -50 0 500 50 0 20 }
}
}]
Which uses the a multiplying pre-factor to put ‘Hrange’ in units of mT. Each line in the Hrange represents a ramping of the simulated magnetic field.
Find out more about using ‘subst’ for variable substitution in OOMMF.
The lines are built up of two 3-value vectors for the start and finish field directions, and the number of steps that should be taken between the start and finish vectors. In other words:
{ Hx_start Hy_start Hz_start Hx_end Hy_end Hz_end num_steps}
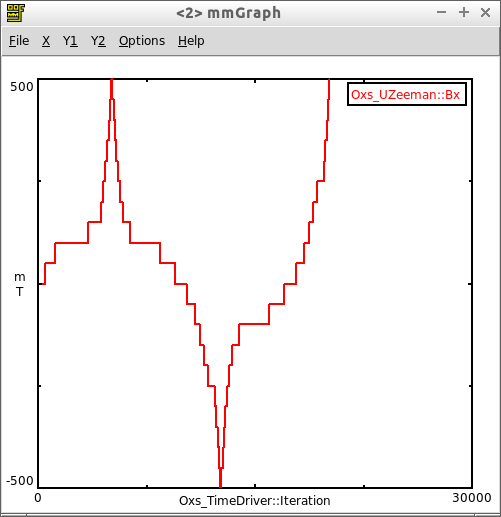
So in this example the field is ramped from 0mT to a field with predominantly positive x component, with some y component in 10 steps. This field is then ramped to an equivalent negative field in 20 steps, before being ramped positive again in a further 20 steps.
Running The Exchspring.mif Example
If we run the exchspring.mif example that comes with oxsi (making sure to capture the output to mmGraph) we can seee that the applied magnetic field changes as the simulation progresses:
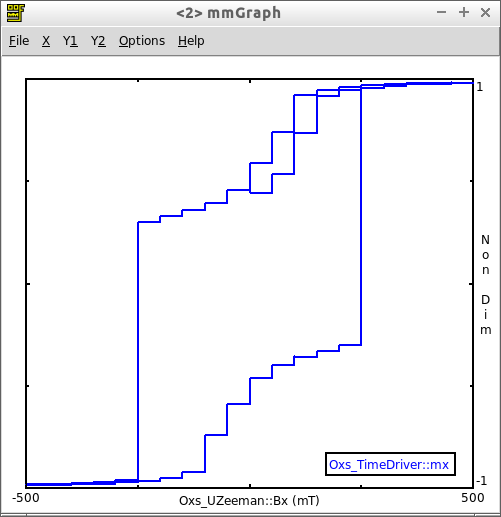
To get the characteristic M-H hystersis loop we just need to plot the magnetisation against the applied magnetic field: